טריגאנאמעטריע

טריגאנאמעטריע (פון גריכיש τρίγωνον טריגאנאן "דרייעק" און μέτρον מעטראן "מעסטן") איז א צווייג פון מאטעמאטיק וואס שטודירט דרייעקן און די פארהעלטענישן צווידן די לענג פון זייערע עקן און די ווינקלען צווישן יענע עקן. טריגאנאמעטריע דעפינירט די טריגאנאמעטרישע פונקציאנען (אויך גערופן קרייזפונקציאנען אדער ווינקל־פונקציאנען), וואס ביישרייבן די פארהעלטענישן, און זענען אנווענדיק צו ציקלישע פענאמענען, ווי למשל כוואליעס. דאס פעלד איז ארויסגעוואקסן אינעם 3טן יארהונדערט פאר דער ציווילער רעכענונג ווי א צווייג פון געאמעטריע שטארק געניצט אין אסטראנאמישע שטודיעס.‏ זי איז אויך די פונדאציע פונעם פראקטישן קונסט פון ערדמעסטונג, און ווערט געניצט אין אפטיק, נאוויגאציע און טעאריע פון מוזיק.

טריגאנאמעטרישע פונקציעס

זעט דעם הויפּט אַרטיקל – טריגאנאמעטרישע פונקציעס

דעפיניציע פון סינוס, קאסינוס, טאנגענט און קאטאנגאנט פון ווינקל α אויפן איינס-קרייז

ס'איז פאראן פארשידענע טריגאנאמעטרישע פונקציעס וואס באשרייבן די פראפארציעס צווישן די עקן פון א גלייכווינקל דרייעק.

אין יעדן גלייכווינקל דרייעק (x צווישן 0° און 90° גראַד אדער צווישן 0 און π/2 ראדיאנען):

• סינוס פון א ווינקל (sin x) דריקט אויס די פראפארציע צווישן דעם קעגנקאטעט (דער עק קעגנאיבער דעם ווינקל) און דעם היפאטענוז, אזוי:

$\sin A={\frac {a}{c}}$

• קאסינוס פון א ווינקל (cos x) דריקט אויס די פראפארציע צווישן דעם אנקאטעט (דער עק לעבן דעם ווינקל) און דעם היפאטענוז:

$\cos A={\frac {b}{c}}$

דער נאמען קאסינוס איז א פארקירצערונג פון complementary sine - סינוס פונעם דערגאנציקן ווינקל.

די פונקציעס באפרידיקן $\cos \alpha =\sin({\frac {\pi }{2}}-\alpha )$           $\sin \alpha =\cos({\frac {\pi }{2}}-\alpha )$

פונעם פיטאגאראס פרינציפ קומט אויס אז דער סכום פון די קוואדראטן פון סינוס און קאסינוס פונעם זעלבן ווינקל באטרעפן 1.

• טאנגענט פון א ווינקל (tg x אדער tan x) איז די פראפארציע צווישן דעם עק קעגנאיבער דעם ווינקל און דעם עק לעבן דעם ווינקל, אזוי:

$\tan A={\frac {a}{b}}$

קומט אויס אז דער טאנגענט איז גלייך מיט דעם סינוס צעטיילט מיטן קאסינוס, און די דעפיניציע ארבעט פאר אלע רעאלע צאלן.

דער היפאטענוז פונעם דרייעק איז דער עק קעגנאיבער דעם גראדווינקל.

מען דעפינירט אויך די אומגעווענדעטע פונקציעס פון די דריי, וואס מ'רופט קאסעקאנט (csc אדער cosec), סעקאנט (sec), און קאטאנגענט (cot):

$\csc A={\frac {1}{\sin A}}={\frac {c}{a}}$

$\sec A={\frac {1}{\cos A}}={\frac {c}{b}}$

$\cot A={\frac {1}{\tan A}}={\frac {\cos A}{\sin A}}={\frac {b}{a}}$

ביישפיל 1: רעכענען די לענג פון אן עק

אין דעם דרייעק ABC ווערט געגעבן די פאלגנדע גרייסן:

$b=5{.}5\,{\mbox{cm}};\quad \alpha =29^{\circ };\quad \gamma =90^{\circ }$

מיט די ווערטן ספעציפיצירט, דארף מען פעסטשטעלן די לענג c. אזוי ווי מען ווייסט דעם אנקאטעט פון $\alpha$, און מען זוכט דעם היפאטענוז, ניצט מען די קאסינוס פונקציע.

$\cos \alpha ={\frac {b}{c}}$

$c={\frac {b}{\cos \alpha }}={\frac {5{.}5\,{\mbox{cm}}}{\cos 29^{\circ }}}=6{.}3\,{\mbox{cm}}$

דער אויסקומפט ווערט פון c איז פארקיילעכט.

ביישפיל 2: רעכענען די גרייס פון א ווינקל

אין דעם דרייעק ABC ווערט געגעבן די פאלגנדע גרייסן:

$a=3{.}1\,{\mbox{cm}};\quad b=5{.}5\,{\mbox{cm}};\quad \gamma =90^{\circ }$

מען דארף פעסטשטעלן דעם ווינקל $\beta$ קעגנאיבער דעם עק b. די ביידע געגעבענ עקן $a$ און $b$ זענען דער אנקאטעט און און גער קעגנקאטעט פון $\beta$. דא פאסט צו ניצן די טאנגענט פונקציע.

$\tan \beta ={\frac {b}{a}}={\frac {5{.}5\,{\mbox{cm}}}{3{.}1\,{\mbox{cm}}}}=1{.}8$

אנשטאט צו רעכענען דעם טאנגענט פון א באוואוסטן ווינקל דארף מען דא אויסטרעפן דעם ווינקל ווייסנדיק דעם טאנגענט. אויף דעם ניצט די פארקערט פונקציע arctan. אזוי קומט אויס:

$\beta =61{.}0^{\circ }$

דער סינוס זאץ און דער קאסינוס זאץ

מיט די אלע פונקציעס קען מען ענטפערן כמעט אלע פראגעס וועגן דרייעקן ווען מען ניצט דעם סינוס זאץ און דעם קאסינוס זאץ. למשל, אז מ'ווייס צוויי עקן און דעם איינגענומענעם ווינקל פון א דרייעק, אדער מ'ווייס אלע דריי עקן, אדער מ'ווייס צוויי ווינקלען און אן עק, קען מען ניצן די צוויי זאצן צו טרעפן די אנדערע עקן און ווינקלען.

א דרייעק ABC

דער סינוס זאץ זאגט אז ביי יעדן דרייעק ABC

${\frac {a}{\sin A}}\,=\,{\frac {b}{\sin B}}\,=\,{\frac {c}{\sin C}}\!$

פארן זעלבן דרייעק, דער קאסינוס זאץ זאגט:

$c^{2}=a^{2}+b^{2}-2ab\cos C$

טריגאנאמעטרישע פונקציעס אויפן איינס קרייז

מען קען פארברייטערן די דעפיניציע פון די טריגאנאמעטרישע פונקציעס פאר אלע רעאלע צאל, נישט נאר פאר ווינקלען אין א גלייכווינקל דרייעק, נאר אויך פאר $\ x\geq 90^{\circ }$ און $\ x\leq 0^{\circ }$, אז מען דעפינירט זיי מיט קאארדינאטן דורך אן איינס קרייז, דאס איז א קרייז מיט צענטער ביים אקסן אנהייב און ראדיוס 1. מען דעפינירט דעם סינוס פונעם ווינקל α ווי דער y- קאארדינאט פונעם פונקט אויפן ארומקרייז פונעם איינס קרייז ווען דער ראדיוס דרייט זיך קעגן דעם זייגער פון דעם פאזיטיוון x-אקס אדורכן ווינקל α, און דער קאסינוס פונעם ווינקל איז דער x- קאארדינאט פון יענעם פונקט. מיט דער דעפיניציע, קומט אויס אז דער סינוס אדער קאסינוס פון א געוויסן ווינקל קענען זיין נעגאטיוו (וואס איז גאנץ אוממעגלעך פאר א ווינקל צווישן 0° און 90°, וואו די פונקציעס זענען א פראפארציע צווישן צוויי לענג), אבער דער סכום פון זייערע קוואדראטן וועט אלעמאל זיין 1. צוליב דעם איז זייער אבסאלוט ווערט פארצוימט דורך 1.

מיט דער דעפיניציע דורכן איינס קרייז קומט אויס אז די טריגאנאמעטרישע פונקציעס זענען פעריאדיש, מיט א פעריאד פון 360 גראד אדער 2π ראדאינען. דאס הייסט אז זייערע ווערטן חזרן זיך איבער נאך די אינטערוואלן. די טאנגענט און קאטאנגענט פונקציעס האבן א פעריאד פון 180 גראד אדער π ראדאינען.

• 
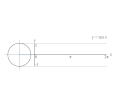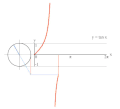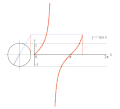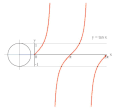
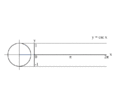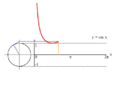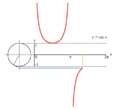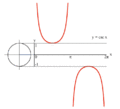
  גראַפֿירן y = sin x דורכן מיטל פון אן איינס קרייז.
• 
  גראַפֿירן y = tan x דורכן מיטל פון אן איינס קרייז.
• 
  גראַפֿירן y = csc x דורכן מיטל פון אן איינס קרייז.

מען קען אויך פארברייטערן די דעפיניציעס פון די טריגאנאמעטרישע פונקציאנען צו קאמפלעקסע צאלן.

אנווענדונגען פון טריגאנאמעטריע

עס זענען פאראן אן א שיעור באניצן פון טריגאנאמעטריע און טריגאנאמעטרישע פונקציעס. צום ביישפיל, די טעכניק פון טריאנגולאציע ווערט געניצט אין אסטראנאמיע צו מעסטן די ווייט פון נאנטע שטערן, אין געאגראפיע צו מעסטן דיסטאנצן צווישן אריענטירן, און אין סאטעליט נאוויגאציע סיסטעמען. די סינוס און קאסינוס פונקציעס זענען יסודותדיק צו דער טעאריע פון פעריאדישע פונקציעס ווי למשל די וואס שילדערן קול און ליכט כוואליעס.

פעלדער וואס ניצן טריגאנאמעטריע אדער טריגאנאמעטרישע פונקציעס שליסן איין אסטראנאמיע (ספעציעל פאר פלאצירן כלומרשטיקע פאזיציעס פון הימלישע אביעקטן, אין וואס ספערישע טריגאנאמעטריע איז נייטיק) און ממילא נאוויגאציע (אויף די אקעאנען, אין עראפלאנען און אינעם קאסמאס), מוזיק טעאריע, אקוסטיק, אפטיק, אנאליז פון פינאנציעלע מארקן, עלעקטראניק, משמעותדיקייט טעאריע, סטאטיסטיק, ביאלאגיע, מעדיצינישע בילדמאכן (קאמפיוטער טאמאגראפיע און אולטראשאל), אפטייקעריי, כעמיע, נומערן טעאריע (און ממילא קריפטאלאגיע), סייסמאלאגיע, מעטעאראלאגיע, אקעאנאגראפיע, ערדמעסטן און געאדעזיע, ארכיטעקטור, פאנעטיק, עקאנאמיק, עלעקטרישע אינזשעניריע, מעכאנישע אינזשעניריע, ציווילע אינזשעניריע, קאמפיוטער גראפיק, קארטאגראפיע און קריסטאלאגראפיע.

באניץ פון טריגאנאמעטריע אין קארטאגראפיע

דער באניץ פון טריגאנאמעטריע איז דער יסוד פון מעסטן פון א שטח—פון אן ערד־שטח פאר בויען ביז א קאנטינענט. א ווינקל איז א זאך וואס מ'קען גאנץ גרינג מעסטן גענוי; דיסטאנצן זענען א סך שווערער צו מעסטן. צוליב דעם, הייבן אן די מעסטער צו איין לענג גאנץ גענוי, דאס איז די באזיס ליניע, וואס איז די ווייט צווישן צוויי באשמימטע פונקטן. נאכדעם שאפט א נעץ פון דרייעקן; מען מעסט די ווינקלען און ניצט טריגאנאמעטריע צו רעכענען די זייטן פון די דרייעקן. אזוי בויט מען אויף א דייטלעכע מאפע פון א גאנצן געגנט. די פראצעדורע ווערט גערופן טריאנגולאציע. כדי צו קאנטראלירן די רעזולטאטן, קען מען מעסטן נאך א דיסטאנץ נאכן אויספירן די טריאנגולאציע.

אין 1751 האט דער אסטראנאם ניקאל לואי דע לאקיי (1713 - 1762) אויסגעפירט אן אויספארש פון מעסטונגען אין דרום אפריקע. זיין הויפט ציל איז געווען צו שאפן א קאטאלאג פון שטערן אין דעם הימל פונעם דרום האלבקיילעך. כדי צו מאכן דאס דייטיק האט ער פריער געדארפט מעסטן דעם בויגן פון א פאסיגן מערידיאן. פאר דעם צוועק האט ער אנטוויקלט א טריאנגולציע פונעם געגנט ביז צפון פון קאפשטאט. זיינע רעזולטאטן האבן געוויזן אז די קרומקייט פון דעם ערד־פלאנעט אין די דרומדיקע גארטל ליניעס איז אסאך ווייניקער ווי אין די צפון דיקע—אן איבערראשנדיקער אויסקומפט וואס מ'האט פעסטגעשטעלט מיט שפעטערע מעסטונגען. קומט אויס אז דער ערד-פלאנעט זעט אויס אין א געוויסן זינען ווי א באר. לאקיי האט געהאט גרויסע הצלחה אין זיין ארבעט צו קאטאלאגירן די שטערן: ער האט געגעבן נעמען צו 15 פון די 88 קאנסטעלאציעס (שטערן גרופעס) וואס זענען אנערקענט היינט. ער האט אבסערווירט מער ווי 10000 שטערן, ניצנדיק א קליין רעפראקציע טעלעסקאפ.

סטאנדארטע אידענטיטען

אן אידענטיטעט איז א גלייכונג וואס איז גילטיק פאר אלע ווערטן.

$\sin ^{2}A+\cos ^{2}A=1\$

$\sec ^{2}A-\tan ^{2}A=1\$

$\csc ^{2}A-\cot ^{2}A=1\$

צולייג פארמלען

$\sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B$

$\cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B$

$\tan(A\pm B)={\frac {\tan A\pm \tan B}{1\mp \tan A\ \tan B}}$

$\cot(A\pm B)={\frac {\cot A\ \cot B\mp 1}{\cot B\pm \cot A}}$

טאפלווינקל פארמלען

$\sin 2A=2\sin A\ \cos A$

$\cos 2A=2\cos ^{2}A-1$

$=\cos ^{2}A\ -\sin ^{2}A$

$=1-2\sin ^{2}A$

$\tan 2A={\frac {2\tan A}{1-\tan ^{2}A}}$

$\cot 2A={\frac {\cot ^{2}A-1}{2\cot A}}$

וועבלינקען

וויקימעדיע קאמאנס האט מעדיע שייך צו: טריגאנאמעטריע